1155. Euclid
From Euclid it is known that for any
positive integers a and b there exist such integers x and y that ax + by = d,
where d is the greatest common
divisor of a and b. The problem is to find for given a and b corresponding x, y
and d.
Input. Each line contains two positive
integers a and b, separated by space (a, b £ 109).
Output. For each test case print in a
separate line three integers x, y and d. If there are several such x
and y, print the pair for which |x| + |y| is minimal. If there also exist multiple answers, print the pair
with minimum x value.
|
Sample input |
Sample output |
4 6
17 17 5 3 |
-1 1 2
0 1 17 -1 2 1 |
SOLUTION
Extended Euclidean algorithm
Algorithm
analysis
Consider the equation: 7x + 9y = 1, where GCD(7,
9) = 1. You must find such pair (x, y) for which |x|
+ |y| is minimal. The answer will be (x, y)
= (4, -3), because 7 * 4 + 9 * (-3) = 1.
Let for positive integers a and b (a > b) we know the
value of g = GCD(b, a mod b), and also the numbers x’
and y’, for which
g = x’ * b
+ y’ * (a mod b)
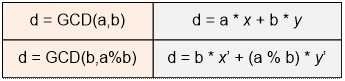
Since a mod b = a - ![]() * b, then
* b, then
g = x’ * b
+ y’ * (a - ![]() * b) = y’
* a + (x’ - y’ *
* b) = y’
* a + (x’ - y’ * ![]() ) * b = x * a + y * b,
) * b = x * a + y * b,
where we denote x = y’, y
= x’ - y’ * ![]() .
.
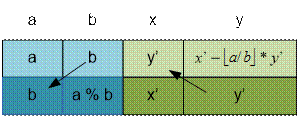
Let gcdext(int
a, int b, int *d, int *x, int *y) be a function that by input numbers a and b finds d
= GCD(a, b) and such x, y that d = a
* x + b * y. To find the unknowns x and y its necessary to
run recursively the function gcdext(b,
a mod b, d, x, y)
and recalculate the values x and y according to the formula above.
The recursion terminates when b = 0. If b = 0, then GCD(a,
0) = a and a = a * 1 + 0 * 0, therefore we put x =
1, y = 0.
Example
Consider the third test case. The GCD(5,
3) calculation and finding the corresponding values of x and y are
given in the table:
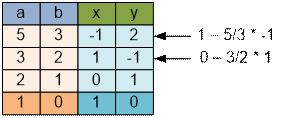
From the table we find that GCD(5, 3)
= 5 * (-1) + 3 * 2 = 1.
Find the
solution to equation 5x + 7y
= 1.
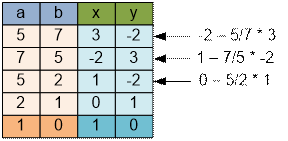
The answer is: GCD(5, 7) = 5 * 3 +
7 * (-2) = 1.
Algorithm realization
Function gcdext by the given a
and b finds such values x, y,
d, that ax + by = d using the extended Euclidean algorithm.
void gcdext(int a, int b, int &d, int &x, int &y)
{
if (b == 0)
{
d = a; x = 1; y = 0;
return;
}
gcdext(b, a % b, d, x, y);
int s = y;
y = x - (a / b) * y;
x = s;
}
The main part of the program. Process
multiple test cases. Read the input data.
while(scanf("%d
%d",&a,&b) == 2)
{
Call the function gcdext and print the
answer.
gcdext(a,b,d,x,y);
printf("%d %d
%d\n",x,y,d);
}
Java realization
import java.util.*;
public class Main
{
static int[] GcdExtended(int a, int b)
{
int res[] = new int[3]; // d, x, y
if (b == 0)
{
res[0] = a; res[1] = 1; res[2] = 0;
return res;
}
res = GcdExtended(b,a % b);
int s = res[2];
res[2] = res[1] - (a / b) * res[2];
res[1] = s;
return res;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
while(con.hasNext())
{
int a = con.nextInt(), b = con.nextInt();
int res[] = GcdExtended(a,b);
System.out.println(res[1] + " " + res[2] + " " + res[0]);
}
}
}